El principio fundamental en el proceso de contar ofrece un método general para contar el numero de posibles arreglos de objetos dentro de un solo conjunto o entre carios conjuntos. Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.
Si un evento A puede ocurrir de n1 maneras y una vez que este ha ocurrido, otro evento B puede n2 maneras diferentes entonces, el número total de formas diferentes en que ambos eventos pueden ocurrir en el orden indicado, es igual a n1 x n2.
2.1.1 Principio Aditivo.
Si se desea llevar a efecto una actividad, la cuál tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas ..... y la última de las alternativas puede ser realizada de W maneras o formas, entonces esa actividad puede ser llevada a cabo de,
M + N + .........+ W maneras o formas
2.1.2 Principio Multiplicativo.
Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:P(A y B) = P(A B) = P(A)P(B) si A y B
Son independientes
P(A y B) = P(A B) = P(A)P(B|A) si A y B
Son dependientes
P(A y B) = P(A B) = P(B)P(A|B) si A y B
Son dependientes
Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N1maneras o formas, el segundo paso de N2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de;
N 1x N 2x..........x N r maneras o formas
El principio multiplicativo implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro.
Son independientes
P(A y B) = P(A B) = P(A)P(B|A) si A y B
Son dependientes
P(A y B) = P(A B) = P(B)P(A|B) si A y B
Son dependientes
Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N1maneras o formas, el segundo paso de N2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de;
N 1x N 2x..........x N r maneras o formas
El principio multiplicativo implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro.
2.1.3 Notación Factorial.
Se usa la notación n! para denotar el producto de los enteros positivos desde 1 hasta n.
1) N! 1 x 2 x 3 x………………… x n
2) 0! =1
3) 1!=1
4) N!=(n-1)! x n
Notación factorial: es el producto de n entero positivo hasta 1.
n! =n (n-1)*(n-2)*(n-3)*«.*3*2*1
En algunos problemas de matemáticas se nos presentan multiplicaciones de números naturales sucesivos tal como: 4 x 3 x 2 x 1 = 24; 3 x 2 x 1 = 6; 2 x 1 = 2.
Para abreviar estas expresiones, se usa una notación especial llamada notación factorial y nos denota las multiplicaciones sucesivas de n hasta 1 y se define como:
4 x 3 x 2 x 1 = 4! Se lee cuatro factorial
3 x 2 x 1 = 3! Se lee tres factorial
En términos generales: (n-1)(n-2)«x 2 x 1 = n! Se lee “n factorial”
2.1.4 Permutaciones.
Hay dos tipos de permutaciones:
Se permite repetir: como la cerradura de arriba, podría ser "333".
Sin repetición: por ejemplo los tres primeros en una carrera. No puedes quedar primero y segundo a la vez.
- Permutaciones con repetición
n × n × ... (r veces) = nr
(Porque hay n posibilidades para la primera elección, DESPUÉS hay n posibilidades para la segunda elección, y así.)
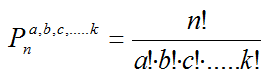
- Permutaciones sin repetición
Por ejemplo, ¿cómo podrías ordenar 16 bolas de billar?
Después de elegir por ejemplo la "14" no puedes elegirla otra vez.
2.1.5 Combinaciones.
También hay dos tipos de combinaciones (recuerda que ahora el orden no importa):
- Se puede repetir: como monedas en tu bolsillo (5,5,5,10,10)
- Sin repetición: como números de lotería (2,14,15,27,30,33)
- Combinaciones con repetición
- Combinaciones sin repetición
La manera más fácil de explicarlo es:
imaginemos que el orden sí importa (permutaciones),
después lo cambiamos para que el orden no importe.
2.1.6 Diagrama de Árbol.
Un diagrama de árbol es una representación gráfica que ilustra las formas en las que se llevan a cabo las agrupaciones de elementos.
C1, C2, C3 y C4 a las diferentes camisetas y P1, P2, P3, P4 y P5 a los distintos pantalones, obtendríamos el diagrama de árbol que se muestra en la figura 1.
Ejemplo:
Una persona tiene 4 camisas de color azul, negro, verde y beige; así mismo tiene 5 pantalones azul marino, negro, gris, beige y café. ¿De cuántas formas diferentes puede vestirse esta persona?
Si llamamos
Si contamos los resultados, comprobamos que obtenemos los 20 que indicaba el principio de la multiplicación.

En los diagramas de árbol se emplea una nomenclatura propia, que describimos a continuación:
C1, C2, C3 y C4.
Árbol: es el diagrama completo.
Raíz: es el punto en el cual se origina el árbol. En la figura, la raíz sería el punto desde donde parten las cuatro flechas que llegan hasta las cuatro opciones de camiseta.
Ramas: son las distintas bifurcaciones. En la figura se corresponden con las flechas del gráfico.
Nodos o nudos: son los puntos desde los que surgen nuevas bifurcaciones. En la figura, los nodos serían los puntos en los que tenemos las 4 opciones de camiseta:
P1, P2, P3, P4 y P5, 20 puntos en total).
Hojas: son los puntos finales, desde los cuales no surgen nuevas bifurcaciones. En la figura, las hojas son los puntos correspondientes a las 5 opciones de pantalón
C1, C2, C3 y C4.
Árbol: es el diagrama completo.
Raíz: es el punto en el cual se origina el árbol. En la figura, la raíz sería el punto desde donde parten las cuatro flechas que llegan hasta las cuatro opciones de camiseta.
Ramas: son las distintas bifurcaciones. En la figura se corresponden con las flechas del gráfico.
Nodos o nudos: son los puntos desde los que surgen nuevas bifurcaciones. En la figura, los nodos serían los puntos en los que tenemos las 4 opciones de camiseta:
P1, P2, P3, P4 y P5, 20 puntos en total).
Hojas: son los puntos finales, desde los cuales no surgen nuevas bifurcaciones. En la figura, las hojas son los puntos correspondientes a las 5 opciones de pantalón
2.1.7 Teorema del Binomio.
El teorema del binomio, también llamado binomio de Newton, expresa la enésima potencia de un binomio como un polinomio. El desarrollo del binomio ( a + b)^n posee singular importancia ya que aparece con mucha frecuencia en Matemáticas y posee diversas
aplicaciones en otras áreas del conocimiento.
FÓRMULA GENERAL DEL BINOMIO
Sea un binomio de la forma (a +b).
Si a este binomio se le multiplica sucesivamente por si mismo se obtienen las siguientes potencias:

Bibliografía.
Institución. (2014). Probabilidades: Principio Aditivo y Multiplicativo. marzo 10, 2017, de Escolares Sitio web: http://www.escolares.net/matematicas/probabilidades-principio-aditivo-y-multiplicativo/
D. Sevilla. (2011). Combinaciones y permutaciones. marzo 10, 2017, de Disfruta Las Matemáticas Sitio web: http://www.disfrutalasmatematicas.com/combinatoria/combinaciones-permutaciones.html
M. Moreno. (2014). Diagramas de árbol en probabilidad. marzo 10, 2017, de MatematicasModernas Sitio web: http://matematicasmodernas.com/diagramas-de-arbol-en-probabilidad/
Joomla. (2014). TEOREMA DEL BINOMIO. marzo 10, 2017, de Joomla! Sitio web: http://www.eneayudas.cl/index.php/alguniv/teobin
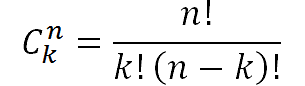
No hay comentarios.:
Publicar un comentario