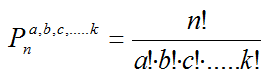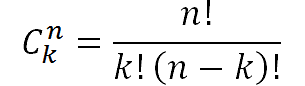Fundamentos de la Teoría de la Probabilidad - Eventos Independientes.

El teorema de Bayes parte de una situación en la que es posible conocer las probabilidades de que ocurran una serie de sucesos Ai.

A esta se añade un suceso B cuya ocurrencia proporciona cierta información, porque las probabilidades de ocurrencia de B son distintas según el suceso Ai que haya ocurrido.

Conociendo que ha ocurrido el suceso B, la fórmula del teorema de Bayes nos indica como modifica esta información las probabilidades de los sucesos Ai.

Ejemplo: Si seleccionamos una persona al azar, la probabilidad de que sea diabética es 0,03. Obviamente la probabilidad de que no lo sea es 0,97.

Si no disponemos de información adicional nada más podemos decir, pero supongamos que al realizar un análisis de sangre los niveles de glucosa son superiores a 1.000 mg/l, lo que ocurre en el 95% de los diabéticos y sólo en un 2% de las personas sanas.

¿Cuál será ahora la probabilidad de que esa persona sea diabética?

La respuesta que nos dá el teorema de bayes es que esa información adicional hace que la probabilidad sea ahora 0,595.

Vemos así que la información proporcionada por el análisis de sangre hace pasar, la probabilidad inicial de padecer diabetes de 0,03, a 0,595.

Evidentemente si la prueba del análisis de sangre hubiese sido negativa, esta información modificaría las probabilidades en sentido contrario. En este caso la probabilidad de padecer diabetes se reduciría a 0,0016.

Bibliografía.

J. Salinas. (2012). Teorema de Bayes. marzo 10, 2017, de URG Sitio web: http://www.ugr.es/~jsalinas/bayes.htm

Fundamentos de la Teoría de la Probabilidad - Ley Multiplicativa.

Para calcular la probabilidad de eventos es necesario que éstos se comporten de una manera más o menos estable. Precisamente, se echa mano de la regularidad estadística, que es la propiedad de los fenómenos aleatorios, y que consiste en que al aumentar el número de repeticiones de un experimento en condiciones prácticamente constantes, la frecuencia relativa de ocurrencia para cada evento tiende a un valor fijo.

Para calcular la probabilidad de un evento se toma en cuenta todos los casos posibles de ocurrencia del evento; es decir, de cuántas formas puede ocurrir determinada situación.

Los casos favorables de ocurrencia de un evento serán los que cumplan con la condición que estoy buscando.

Así para el tiro de una moneda tengo 2 casos posibles de ocurrencia (o cae águila o cae sol) y sólo 1 caso favorable de que pueda caer águila (pues sólo hay un águila en la moneda).

Para calcular la probabilidad de un evento se utiliza la siguiente fórmula:

Para nuestro ejemplo: Probabilidad de "que caiga un águila" tenemos

Por lo tanto, existe una probabilidad del 50% que yo obtenga un águila al tirar una moneda.

Veamos otro ejemplo: Si yo tengo una canasta llena de peras y manzanas, de las cuales hay 20 peras y 10 manzanas. ¿Qué fruta es más probable que saque al azar de la canasta?

Para este ejemplo tenemos que 30 es el total de frutas en la canasta; es decir los casos posibles. Para calcular la probabilidad de sacar una manzana mis casos favorables son 10 puesto que existen sólo 10 manzanas. Así, aplicando la fórmula obtenemos que:

Como 66.7 es mayor que 33.3 es más probable que saque una pera, pues hay más peras que manzanas en la canasta.

Fíjate bien que 33.3% + 66.7% es igual al 100% porque siempre que saques algo de la canasta es seguro que saques una fruta.

Así, el valor de la probabilidad de un evento imposible es 0 mientras que la probabilidad de un evento seguro es 1; porque:

Bibliografía.

Institución.. (2014). Ley multiplicativa. marzo 10, 2017, de Jimdo Sitio web: https://wape23.jimdo.com/unidad-2/2-6-ley-multiplicativa/

Fundamentos de la Teoría de la Probabilidad - Probabilidad Condicional.

Eventos dependientes.

Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(A|B) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.

Eventos Independientes.

Dos o más eventos son independientes cuando la ocurrencia o no-ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Un caso típico de eventos independiente es el muestreo con reposición, es decir, una vez tomada la muestra se regresa de nuevo a la población donde se obtuvo.

Ejemplo:

lanzar al aire dos veces una moneda son eventos independientes por que el resultado del primer evento no afecta sobre las probabilidades efectivas de que ocurra cara o sello, en el segundo lanzamiento.

Bibliografía.

Y. Alvarado, (2014), marzo 10, 2017, http://probabilidadmitad1.blogspot.mx/p/eventos-dependientes-e-independientes.html

Fundamentos de la Teoría de la Probabilidad - Probabilidad con Técnicas de Conteo.

Axiomas

Los axiomas de probabilidad son las condiciones mínimas que deben verificarse para que una función definida sobre un conjunto de sucesos determine consistentemente sus probabilidades. Fueron formulados por Kolmogórov en 1933.

Los axiomas de la formulación moderna de la teoría de la probabilidad constituyen una base para deducir a partir de ellas un amplio número de resultados.

La letra P se utiliza para designar la probabilidad de un evento, siendo P(A) la probabilidad de ocurrencia de un evento A en un experimento.


AXIOMA 1
Si A es un evento de S, entonces la probabilidad del evento A es:
0 ≤ P(A) ≤ 1
Como no podemos obtener menos de cero éxitos ni más de n éxitos en n experimentos, la
probabilidad de cualquier evento A, se representa mediante un valor que puede variar de 0 a 1.


AXIOMA 2
Si dos eventos son mutuamente excluyentes, la probabilidad de obtener A o B es igual a la
probabilidad de obtener A más la probabilidad de obtener B.
P(A ∪ B) = P(A) + P(B)
Excluirse mutuamente quiere decir que A y B no pueden ocurrir simultáneamente en el mismo experimento. Así, la probabilidad de obtener águila o sol en la misma tirada de una moneda será
P(A ∪ B) = P(A) + P(B)
P(A ∪ B) = 1/2 + 1/2 = 1.
En general podemos decir que la suma de las probabilidades de todos los posibles eventos
mutuamente excluyentes es igual a 1:
P(A1) + P(A2) + P(A3) + ... + P(An) = 1


AXIOMA 3
Si A es un evento cualquiera de un experimento aleatorio y A’ es el complemento de A, entonces:
P(A’) = 1 - P(A)
Es decir, la probabilidad de que el evento A no ocurra, es igual a 1 menos la probabilidad de que ocurra.



TEOREMAS

TEOREMA 1. Si f es un evento nulo o vacío, entonces la probabilidad de que ocurra f debe ser cero.


p(f)=0

DEMOSTRACIÓN:
Si sumamos a fun evento A cualquiera, como f y A son dos eventos mutuamente excluyentes, entonces p(AfÈ)=p(A) +p(f)=p(A). LQQD


TEOREMA 2. La probabilidad del complemento de A, Ac debe ser, p(Ac)= 1 – p(A)


DEMOSTRACIÓN:
Si el espacio muestral d, se divide en dos eventos mutuamente exclusivos, A y Ac luego d=AÈAc, por tanto p(d)=p(A) + p(Ac) y como en el axioma dos se afirma que p(d)=1, por tanto, p(Ac)= 1 - p(A) .LQQD


TEOREMA 3. Si un evento A Ì B, entonces la p(A) £ p(B).

DEMOSTRACIÓN:
Si separamos el evento B en dos eventos mutuamente excluyentes, A y B \ A (B menos A), por tanto, B=AÈ(B \ A) y p(B)=p(A) +p(B \ A), luego entonces si p(B \ A)³0 entonces se cumple que p(A)£p(B). LQQD


TEOREMA 4. La p( A \ B )= p(A) – p(AÇB)



DEMOSTRACIÓN: Si A y B son dos eventos cualquiera, entonces el evento A se puede separar en dos eventos mutuamente excluyentes, (A \ B) y AÇB, por tanto, A=(A \ B)È(AÇB), luego p(A)=p(A \ B) + p(AÇB), entonces, p(A \ B) = p(A) – p(AÇB). LQQD


TEOREMA 5. Para dos eventos A y B, p(AÈB)=p(A) + p(B) – p(AÇB).



DEMOSTRACIÓN:

Si AÈB = (A \ B) È B, donde (A \ B) y B son eventos mutuamente excluyentes, por lo que p(A È B) = p(A \ B) + p(B) y del teorema anterior tomamos que p(A \ B) = p(A) – p(AÇB), por tanto, p(AÈB) = p(A) + p(B) – p(AÇB). LQQD

Bibliografía.

J. Morales, (2012), marzo 10, 2017 http://probabilidadyestadisticaitsav.blogspot.mx/2012/06/23-probabilidad-con-tecnicas-de-conteo.html

Fundamentos de la Teoría de la Probabilidad - Probabilidad de Eventos.

Definición del Espacio Muestral.

Es el conjunto de todos los posibles resultados de un experimento. En la definición anterior, el espacio muestral Ω consta de n elementos (puntos muestrales). 

Definición de Evento.

En la teoría de la probabilidad, un evento aleatorio o suceso aleatorio es un subconjunto de un espacio muestral, es decir, un conjunto de posibles resultados que se pueden dar en un experimento aleatorio. En teoría de la probabilidad a cada evento aleatorio se le puede asignar una medida de probabilidad, y el conjunto de todos los sucesos aleatorios constituye una σ-álgebra de conjuntos.

Simbología.

La simbología que se usa para simplificar y representar las relaciones que existen entre distintos conjuntos de cosas, es importante conocer el significado de cada una de ellas para poder interpretar diferentes formulas.

Es importante saber que u representa a universo de conjuntos de que estamos hablando, por ejemplo si hablamos de numero de pares, el universo seria todos los números y estos números pares serian un conjunto del universo.

Los conjuntos los podemos representar con letras mayúsculas y los elementos de este conjunto se representan con letras minúsculas o numero según se necesite, además de que deberán estar entre llaves. Como el siguiente ejemplo:

A=(1,2,3,4,5,6)

Aquí podremos ver que el conjunto está representados por la letra A y los números 1,2,3,4,5,6 pertenecen o están dentro de este conjunto

Y=(a,b,c,d,e)

De igual manera en el ejemplo anterior

Pero no solamente podemos representar por medio de simbología, los conjuntos de manera aislada, sino que además podemos, representar las operaciones que se pueden realizar entre ellos.

Bibliografía.

M. Delgado. (2015). Espacio Muestral. marzo 10, 2017, de thales Sitio web: http://thales.cica.es/rd/Recursos/rd99/ed99-0278-01/probab1.html

M. Paret. (2016). Probabilidad del evento. marzo 10, 2017, de Minitab Inc Sitio web: http://support.minitab.com/es-mx/minitab/17/topic-library/modeling-statistics/regression-and-correlation/logistic-regression/event-probability/

Fundamentos de la Teoría de la Probabilidad - Teoría Elemental de la Probabilidad.

La teoría elemental de la probabilidad nos permite comprender de manera precisa la incertidumbre. Con este conocimiento nos podemos ayudar a hacer predicciones. tomar mejores decisiones, valorar los riesgos incluso hasta ganar dinero. En conclusión decimos que la probabilidad se utiliza para determinar cuan probable es un determinado evento.

Concepto Clásico y Relación con la frecuencia Relativa.

La definición clásica de la probabilidad, en su forma actual, esta basada en el concepto de equiprobabilidad de los resultados, basado a su vez en la simetría. Se supone que un experimento se puede descomponer en n sucesos equiprobables y mutuamente excluyentes E1,...En, llamados sucesos 'Elementales'. Asi la probabilidad de suceso aleatorio A es el número del intervalo [0,1] que expresa el cociente entre los m sucesos elementales que componen A y el número total n de posibles sucesos elementales. El principal escollo que encuentra esta interpretación de la probabilidad es la dificultad de descomponer un suceso en sucesos equiprobables elementales; siendo fácil para problemas sencillos, como los de las cartas, dados o urnas, es casi imposible para problemas más complejos.

Basándose en los trabajos de Graunt y Petty, Bernouli resolvió incluso la cuestión de cómo hallar la probabilidad de ocurrencia de un suceso aun siendo imposible contar los casos favorables.

De esta manera Bernouli introdujo el concepto de probabilidad "frecuentista" o "estadística": asignar como probabilidad de un suceso el resultado que se obtendría si el procesos se repitiera en condiciones un número grande de veces. Sin embargo, estas condiciones son demasiado vagas para servir como base para una definición científica rigurosa. En primer lugar, se menciona un numero grande de veces, pero no se da ninguna indicación sobre cuál es ese numero lo suficientemente grande; no se describe con precisión que se entiende por condiciones similares si las condiciones fuesen siempre exactamente las mismas se obtendría siempre el mismo resultado; tampoco se especifica cual es la máxima desviación admitida respecto del resultado teórico, además sigue habiendo sucesos que no pueden plantearse suponiendo la posibilidad de repetirlos muchas veces.

Precisamente, fueron la necesidad de precisar qué se entiende por "un numero grande"de repeticiones del experimento y la tolerancia del resultado obtenido respecto del teórico, lo que llevaron a Jakob Bernoulli a idear, en su forma más intuitiva y básica, la Ley dee los Grandes Números.

P(A)= nA/n

Cantidad de resultados que implican la aparición de A entre la Cantidad total de resultados.

La Interpretación Subjetiva de la probabilidad

En el segundo cuarto del siglo XX surgió una nueva interpretación, llamada subjetiva, según la cual la probabilidad mide el grado de creencia de un individuo en la verdad de una proposición, variando entre 0 (el individuo cree que es falso) a 1 ( cree que es cierto).

Esta interpretación fue propuesta por primera vez por el filósofo Frank P. Ramsey en su libro Los fundamentos de las matemáticas de 1931, y el primer matemático que la adoptó fue el estadístico italiano Bruno de Finetti en 1937. La interpretación subjetiva de la probabilidad es más amplia que la frecuencia, pues mientras que ésta solo funciona con experimentos que puedan repetir un numero grande de veces, aquélla se puede aplicar a cualquier tipo de proposiciones.

Además, mientras que los frecuentistas consideran que la probabilidad de un suceso es siempre una constante, para los subjetivistas la probabilidad de un suceso puede y debe variar en función de la nueva información recibida respecto del suceso, manera de proceder que se ajusta más al método científico.

Una crítica que se ha hecho de la interpretación subjetiva es la supuesta arbitrariedad con que se asignan probabilidades a sucesos. Los subjetivistas se defienden afirmando que las normas de la mora y la coherencia obligan a quien asigna la probabilidad de un suceso a actuar del modo mas objetivo posible y no de forma caprichosa. Además, se han hecho esfuerzos para convertir esta noción intuitiva en demostraciones formales

Bibliografía.

J. Aguilar. (2010). Probabilidad y Estadistica. marzo 10, 2017, de Jimdo Sitio web: https://wape23.jimdo.com/unidad-2/2-1-teor%C3%ADa-elemental-de-la-probabilidad/2-1-2-la-interpretaci%C3%B3n-subjetiva-de-la-probabilidad/

Fundamentos de la Teoría de la Probabilidad - Técnicas de Conteo.

El principio fundamental en el proceso de contar ofrece un método general para contar el numero de posibles arreglos de objetos dentro de un solo conjunto o entre carios conjuntos. Las técnicas de conteo son aquellas que son usadas para enumerar eventos difíciles de cuantificar.

Si un evento A puede ocurrir de n1 maneras y una vez que este ha ocurrido, otro evento B puede n2 maneras diferentes entonces, el número total de formas diferentes en que ambos eventos pueden ocurrir en el orden indicado, es igual a n1 x n2.

2.1.1 Principio Aditivo.

Si se desea llevar a efecto una actividad, la cuál tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas ..... y la última de las alternativas puede ser realizada de W maneras o formas, entonces esa actividad puede ser llevada a cabo de,

M + N + .........+ W maneras o formas

2.1.2 Principio Multiplicativo.

Se relacionan con la determinación de la ocurrencia de conjunta de dos o más eventos. Es decir la intersección entre los conjuntos de los posibles valores de A y los valores de B, esto quiere decir que la probabilidad de que ocurran conjuntamente los eventos A y B es:P(A y B) = P(A B) = P(A)P(B) si A y B

Son independientes
P(A y B) = P(A B) = P(A)P(B|A) si A y B

Son dependientes
P(A y B) = P(A B) = P(B)P(A|B) si A y B

Son dependientes
Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N1maneras o formas, el segundo paso de N2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de;

N 1x N 2x..........x N r maneras o formas

El principio multiplicativo implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro.

 

2.1.3 Notación Factorial.

Se usa la notación n! para denotar el producto de los enteros positivos desde 1 hasta n.

1) N! 1 x 2 x 3 x………………… x n

2) 0! =1

3) 1!=1

4) N!=(n-1)! x n

Notación factorial: es el producto de n entero positivo hasta 1.

n! =n (n-1)*(n-2)*(n-3)*«.*3*2*1

En algunos problemas de matemáticas se nos presentan multiplicaciones de números naturales sucesivos tal como: 4 x 3 x 2 x 1 = 24; 3 x 2 x 1 = 6; 2 x 1 = 2.

Para abreviar estas expresiones, se usa una notación especial llamada notación factorial y nos denota las multiplicaciones sucesivas de n hasta 1 y se define como:

4 x 3 x 2 x 1 = 4! Se lee cuatro factorial

3 x 2 x 1 = 3! Se lee tres factorial

En términos generales: (n-1)(n-2)«x 2 x 1 = n! Se lee “n factorial”

2.1.4 Permutaciones.

Hay dos tipos de permutaciones:
Se permite repetir: como la cerradura de arriba, podría ser "333".
Sin repetición: por ejemplo los tres primeros en una carrera. No puedes quedar primero y segundo a la vez.

• Permutaciones con repetición

Son las más fáciles de calcular. Si tienes n cosas para elegir y eliges r de ellas, las permutaciones posibles son:

n × n × ... (r veces) = nr
(Porque hay n posibilidades para la primera elección, DESPUÉS hay n posibilidades para la segunda elección, y así.)

• Permutaciones sin repetición

En este caso, se reduce el número de opciones en cada paso.

Por ejemplo, ¿cómo podrías ordenar 16 bolas de billar?
Después de elegir por ejemplo la "14" no puedes elegirla otra vez.

2.1.5 Combinaciones.

También hay dos tipos de combinaciones (recuerda que ahora el orden no importa):

• Se puede repetir: como monedas en tu bolsillo (5,5,5,10,10)
• Sin repetición: como números de lotería (2,14,15,27,30,33)

1. Combinaciones con repetición

En realidad son las más difíciles de explicar, así que las dejamos para luego.

1. Combinaciones sin repetición

Así funciona la lotería. Los números se eligen de uno en uno, y si tienes los números de la suerte (da igual el orden) ¡entonces has ganado!

La manera más fácil de explicarlo es:
imaginemos que el orden sí importa (permutaciones),
después lo cambiamos para que el orden no importe.

2.1.6 Diagrama de Árbol.

Un diagrama de árbol es una representación gráfica que ilustra las formas en las que se llevan a cabo las agrupaciones de elementos.
C1, C2, C3 y C4 a las diferentes camisetas y P1, P2, P3, P4 y P5 a los distintos pantalones, obtendríamos el diagrama de árbol que se muestra en la figura 1.
Ejemplo:
Una persona tiene 4 camisas de color azul, negro, verde y beige; así mismo tiene 5 pantalones azul marino, negro, gris, beige y café. ¿De cuántas formas diferentes puede vestirse esta persona?

Si llamamos
Si contamos los resultados, comprobamos que obtenemos los 20 que indicaba el principio de la multiplicación.

En los diagramas de árbol se emplea una nomenclatura propia, que describimos a continuación:
C1, C2, C3 y C4.
Árbol: es el diagrama completo.

Raíz: es el punto en el cual se origina el árbol. En la figura, la raíz sería el punto desde donde parten las cuatro flechas que llegan hasta las cuatro opciones de camiseta.

Ramas: son las distintas bifurcaciones. En la figura se corresponden con las flechas del gráfico.

Nodos o nudos: son los puntos desde los que surgen nuevas bifurcaciones. En la figura, los nodos serían los puntos en los que tenemos las 4 opciones de camiseta:
P1, P2, P3, P4 y P5, 20 puntos en total).
Hojas: son los puntos finales, desde los cuales no surgen nuevas bifurcaciones. En la figura, las hojas son los puntos correspondientes a las 5 opciones de pantalón

 

2.1.7 Teorema del Binomio.

El teorema del binomio, también llamado binomio de Newton, expresa la enésima potencia de un binomio como un polinomio. El desarrollo del binomio ( a + b)^n posee singular importancia ya que aparece con mucha frecuencia en Matemáticas y posee diversas
aplicaciones en otras áreas del conocimiento.

FÓRMULA GENERAL DEL BINOMIO
Sea un binomio de la forma (a +b).

Si a este binomio se le multiplica sucesivamente por si mismo se obtienen las siguientes potencias:

Bibliografía.

Institución. (2014). Probabilidades: Principio Aditivo y Multiplicativo. marzo 10, 2017, de Escolares Sitio web: http://www.escolares.net/matematicas/probabilidades-principio-aditivo-y-multiplicativo/

D. Sevilla. (2011). Combinaciones y permutaciones. marzo 10, 2017, de Disfruta Las Matemáticas Sitio web: http://www.disfrutalasmatematicas.com/combinatoria/combinaciones-permutaciones.html

M. Moreno. (2014). Diagramas de árbol en probabilidad. marzo 10, 2017, de MatematicasModernas Sitio web: http://matematicasmodernas.com/diagramas-de-arbol-en-probabilidad/

Joomla. (2014). TEOREMA DEL BINOMIO. marzo 10, 2017, de Joomla! Sitio web: http://www.eneayudas.cl/index.php/alguniv/teobin